Answer:
The angle ACB is 9 degrees.
Explanation:
To solve this problem we just need to observe the point B, which has two angles and both of them are on a straight angle, this means that the sum of angle ABC and CBD is 180, that is
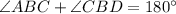
We know that
 , then
, then
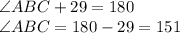
Now, in the triangle ABC, we know that all three angles must sum 180
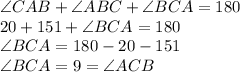
Therefore, the angle ACB is 9 degrees.