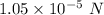Question

Two identical conducting small spheres are placed with their centers 0.395 m apart. One is given a charge of -12.0 nC and the other a charge of -15.0 nC.

(a) Find the electric force exerted by one sphere on the other.(magnitude)
(b) The spheres are connected by a conducting wire. Find the electric force each exerts on the other after they have come to equilibrium. (magnitude)

Answer 1

(a). The magnitude of the electric force exerted by one sphere on the other is
`10.38*10^(-6)\ N`

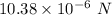
(b). The electric force each exerts on the other after they have come to equilibrium is
`1.05*10^(-5)\ N`

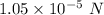
Step-by-step explanation:

Given that,

Distance = 0.395 m

Charge of first sphere = -12.0 nC

Charge of second sphere = -15.0 nC

(a). We need to calculate the magnitude of the electric force exerted by one sphere on the other

Using formula of electric force

`F=(kq_(1)q_(2))/(r^2)`

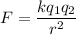
Where,
`q_(1)=-12.0\ nC`

`q_(2)=-15.0\ nC`

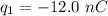
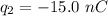
r = distance

Put the value into the formula

`F=(9*10^(9)*12.0*10^(-9)*15*10^(-9))/((0.395)^2)`

`F=10.38*10^(-6)\ N`

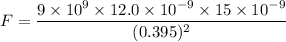
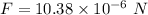
(b). The identical spheres are connected by a conducting wire.

Both charges are same so the force is repulsive.

We need to calculate the net charge

Using formula of charge

`Q=(q_(1)+q_(2))/(2)`

Put the value into the formula

`Q=((-12.0-15.0)*10^(-9))/(2)`

`Q=-13.5*10^(-9)\ C`

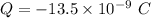
We need to calculate the magnitude of the electric force each exerts on the other after they have come to equilibrium

Using formula of electric force

`F=(kQ^2)/(r^2)`

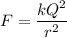
Put the value into the formula

`F=(9*10^(9)*(-13.5*10^(-9))^2)/((0.395)^2)`

`F=1.05*10^(-5)\ N`

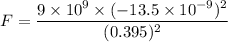
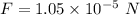
Hence, (a). The magnitude of the electric force exerted by one sphere on the other is
`10.38*10^(-6)\ N`

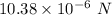
(b). The electric force each exerts on the other after they have come to equilibrium is
`1.05*10^(-5)\ N`

Answer 2

a)
`F=1.04* 10^(-5)\ N=1.04\ dyne`

b)
`F=1.05* 10^(-5)\ N=1.05\ dyne`

Step-by-step explanation:

Given:

• charge
  `q_1=-12* 10^(-9)\ C`

• charge
  `q_2=-15* 10^(-9)\ C`

• distance between the charges,
  `d=0.395\ m`

a)

Now we know from the Coulombs law:

`F=(1)/(4\pi.\epsilon_0) * (q_1.q_2)/(d^2)`

`F=9* 10^9 * (12* 10^(-9)* 15* 10^(-9))/(0.395^2)`

`F=1.04* 10^(-5)\ N=1.04\ dyne`

b)

On connecting the two charges via a conductor the two charges come to equilibrium.

`F=9* 10^9* (13.5* 10^(-9)* 13.5* 10^(-9))/(0.395^2)`

`F=1.05* 10^(-5)\ N=1.05\ dyne`