Question

Modeling Radioactive Decay In Exercise, complete the table for each radioactive isotope.

Amount Amount
after after
Half-life Initial 1000 10,000
Isotope (In years) quantity years years
239Pu 24,100 2.4 grams

Answer 1

The amount after 1000 years will be, 2.33 grams.

The amount after 10000 years will be, 1.80 grams.

Step-by-step explanation :

Half-life = 24100 years

First we have to calculate the rate constant, we use the formula :

`k=(0.693)/(t_(1/2))`

`k=\frac{0.693}{24100\text{ years}}`

`k=2.88* 10^(-5)\text{ years}^(-1)`

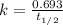
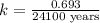
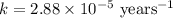
Now we have to calculate the amount after 1000 years.

Expression for rate law for first order kinetics is given by:

`t=(2.303)/(k)\log(a)/(a-x)`

where,

k = rate constant =
`2.88* 10^(-5)\text{ years}^(-1)`

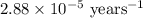
t = time passed by the sample = 1000 years

a = initial amount of the reactant = 2.4 g

a - x = amount left after decay process = ?

Now put all the given values in above equation, we get

`1000=(2.303)/(2.88* 10^(-5))\log(2.4)/(a-x)`

`a-x=2.33g`

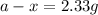
Thus, the amount after 1000 years will be, 2.33 grams.

Now we have to calculate the amount after 10000 years.

Expression for rate law for first order kinetics is given by:

`t=(2.303)/(k)\log(a)/(a-x)`

where,

k = rate constant =
`2.88* 10^(-5)\text{ years}^(-1)`

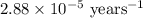
t = time passed by the sample = 10000 years

a = initial amount of the reactant = 2.4 g

a - x = amount left after decay process = ?

Now put all the given values in above equation, we get

`10000=(2.303)/(2.88* 10^(-5))\log(2.4)/(a-x)`

`a-x=1.80g`

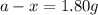
Thus, the amount after 10000 years will be, 1.80 grams.