Answer:
A 30 meter high building sits on top of a hill. The angles of elevation of the top an bottom of the building from the same spot at the base of the hill are measured to be 55 degrees and 50 degrees respectively. The height of the hill to the nearest meter is 151 meter.
Step-by-step explanation:
Given, Height of the building on top of a hill = 30 meter
The angel of elevation of the top of the building from a spot at the base of hill = 55 degrees
The angel of elevation of the bottom of the building from the same spot at the base of hill = 50 degrees
The given scenario is shown in the below attachment.
Let us consider the height of hill be 'h' and distance between the base of the hill and the spot of elevation be 'x'.
From the figure,
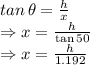 .... (1)
.... (1)
and
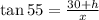
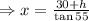
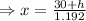 .... (2)
.... (2)
[
 tan 50 = 1.192 and tan 55 = 1.428]
tan 50 = 1.192 and tan 55 = 1.428]
Since the distance between the base of the hill and the spot is same for both elevations, equating equations (1) and (2), we get
By cross-multiplying, we get
(30 + h)1.192 = 1.428h
35.76 + 1.192h = 1.428h
1.428h - 1.192h = 35.76
0.236h = 35.76
h = 151.52 meter
Thus, the height of the hill to the nearest meter is 151 meter.