Answer:
a)
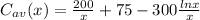
b)
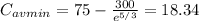
Explanation:
a) In order to solve this part of the problem we must remember that the average cost function is found by using the following formula:
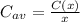
so all we need to do is to divide the cost function into x, so we get:
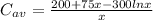
which yields:

b) In order to find the minimum average cost analytically, we must use the first derivative to find the local minima, so we proceed and find the derivative of the average cost function. We can rewrite the function so it is easier for us to find:

we will need to find the derivative of a fraction so we will be using the quotient rule to do so, the quotient rule goes as follows:
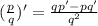
in this case we get that:
p=lnx
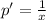
q=x
q'=1
so when using the formula we get that the derivative of
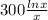 is:
is:
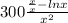
which simplifies to:
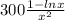
so the whole derivative of the average cost function turns out to be:
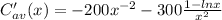
Which can be rewritten as:
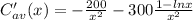
so now we can set it equal to zero to solve for x, so we get that:
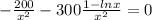
So now we multiply both sides of the equation by
 .
.
so we get:
-200-300+300ln x=0
300lnx=500
so:
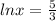
so the answer is:

Now we need to determine if this is a local max or min. We can do so by using the second derivative test, so we take the second derivative of the average cost function:
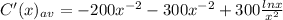
which simplifies to:
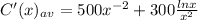
so now we can take the second derivative of this function, the second fraction is differentiated the same way as in the first time, so we get:
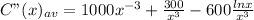
we can go ahead and solve this second derivative for x=5.294 which yields:
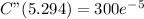
notice we get a positive answer, which means that the graph is concave up at that very point. This means this is a local minimum.
So the minimum average cost will be:

which yields:
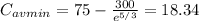
Which can be located in the graph when plotting it. See attached picture.