Analyzing a Graph In Exercise, analyze and sketch the graph of the function. Label any relative extrema, points of inflection, and asymptotes. y = 8 In x/x^2

Question

asked Aug 5, 2021 230k views

1 Answer

Sharif Amlani · Answer 1 · 2021-08-08T20:46:10+0000

Answer:

Analyzed ans Sketched.

Explanation:

We are given the function:

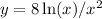
$y = 8 \ln (x)/x^2$

The first derivative of y:

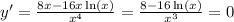
$y' = (8x-16x\ln(x))/(x^4) =(8-16\ln(x))/(x^3) =0$

The root
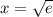$x = \sqrt e$ is absolute maximum.

The second derivative of y:

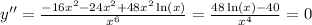
$y''=(-16x^2-24x^2+48x^2\ln(x))/(x^6) =(48\ln(x)-40)/(x^4) =0$

The root
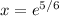x = e^(5/6) is point where concavity changes from down to up.

x = 0 is vertical asymptote.

y = 0 is horizontal asymptote.

The sketch is given in the attachment.