Question

Giving 65 Points for correct answer TODAY, finals are tomorrow!

Consider the diagram


1. Which theorem can be used to prove that the triangles are similar?





2. Write a similarity statement for the triangles.





3. Find the values of x and y. Show your work!

Answer 1

Therefore

1. Vertical Opposite Angle Theorem is used to prove that the triangles are similar.

2. Angle-Angle similarity statement is used.

3. x = 10 unit and y = 7.5 unit.

Explanation:

Given:

∠A ≅ ∠E

AB = 8 , DE = 12 , BC = 5 , CE = 15

To Prove:

Δ ABC ~ ΔEDC

To Find :

x = ?

y = ?

Proof:

Vertical Angle Theorem:

The angles opposite each other when two lines cross. They are always equal.

Here vertical opposite angles are,

∴ ∠ACB ≅ ∠ECD

Angle-Angle Similarity :

If in Two triangle Two corresponding angles are congruent then the Triangles are Similar by Angle-Angle Similarity statement.

Now,

In Δ ABC and Δ EDC

∠A ≅ ∠E …………..{ Given }

∠ACB ≅ ∠ECD ……….....{Vertical Opposite Angle Theorem}

Δ ABC ~ Δ EDC ….{Angle-Angle Similarity test}

If two triangles are similar then their sides are in proportion.

`(AB)/(ED) =(BC)/(DC)=(AC)/(EC)\textrm{corresponding sides of similar triangles are in proportion}\\`

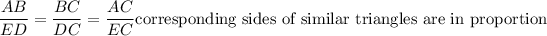
On Substituting the given values we get

`(8)/(12) =(5)/(y)=(x)/(15)`

Therefore,

`(8)/(12) =(5)/(y)\\\\y=(60)/(8)=7.5\\\\y=7.5\ unit`

`(8)/(12) =(x)/(15)\\\\\therefore x=(120)/(12)\\\\\x=10`

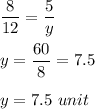
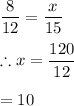
Therefore

1. Vertical Opposite Angle Theorem is used to prove that the triangles are similar.

2. Angle-Angle similarity statement is used.

3. x = 10 unit and y = 7.5 unit.