Answer: The probability that Xavier and Yvonne can solve a problem but Zelda cannot is

Explanation:
We are given:
Probability of success of Xavier,
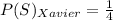
Probability of failure of Xavier,
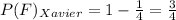
Probability of success of Yvonne,
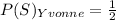
Probability of failure of Yvonne,
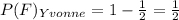
Probability of success of Zelda,
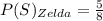
Probability of failure of Zelda,
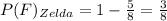
We need to calculate:
The probability that Xavier and Yvonne can solve the problem but Zelda cannot, we use:
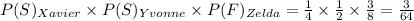
Hence, the probability that Xavier and Yvonne can solve a problem but Zelda cannot is
