Question

Use integration by parts to derive the following formula from the table of integrals.

∫x^n . ln |x|dx=x^n+1 [ln |x|/n+1]-1/(n+1)^2]+c, n≠-1.

Answer 1

`ln|x|((x^(n+1))/(n+1))-(x^(n+1))/((n+1)^2)+C,n\\eq -1`

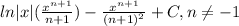
Explanation:

We have been given an indefinite integral
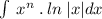`\int \:x^n\:.\:ln\:|x|dx`. We are asked to integrate it.

We will use integration by pats to solve our given problem.

`\int udvdx=uv-\int vdu`

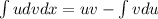
Let
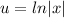`u=ln|x|` and
`v'=x^n`.

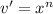Now, we need to find du and v using above values.

`(du)/(dx)=(1)/(x)`

`du=(1)/(x)dx`

`v'=x^n`

`v=(x^(n+1))/(n+1)`

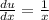
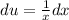
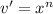
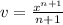
Substitute these values in integration by parts formula:

`\int \:x^n\:.\:ln\:|x|dx=ln|x|((x^(n+1))/(n+1))-\int (x^(n+1))/(n+1)*(1)/(x)dx`

`\int \:x^n\:.\:ln\:|x|dx=ln|x|((x^(n+1))/(n+1))-\int (x^(n+1))/(n+1)*x^(-1)dx`

`\int \:x^n\:.\:ln\:|x|dx=ln|x|((x^(n+1))/(n+1))-(1)/(n+1)\int x^(n+1-1)dx`

`\int \:x^n\:.\:ln\:|x|dx=ln|x|((x^(n+1))/(n+1))-(1)/(n+1)\int x^(n)dx`

`\int \:x^n\:.\:ln\:|x|dx=ln|x|((x^(n+1))/(n+1))-(1)/(n+1)*(x^(n+1))/(n+1)+C`

`\int \:x^n\:.\:ln\:|x|dx=ln|x|((x^(n+1))/(n+1))-(x^(n+1))/((n+1)^2)+C,n\\eq -1`

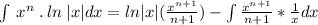
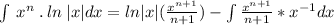
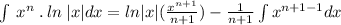
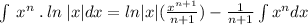
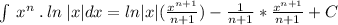
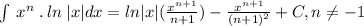
Therefore, our required integral would be
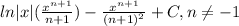`ln|x|((x^(n+1))/(n+1))-(x^(n+1))/((n+1)^2)+C,n\\eq -1`.