Answer:
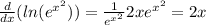
Explanation:
For this case we want to find the derivate of this function:
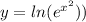
And in order to find the derivate we need to apply the chain rule given by:
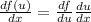
And on this case
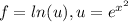
And we can find the partial derivates like this:
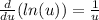
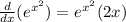
And if we replace we got:
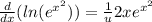
And if we replace
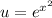 we got:
we got:
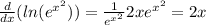
And that would be our final answer on this case