Question

The box plots below show the average daily temperatures in April and October for a U.S. city: two box plots shown. The top one is labeled April. Minimum at 50, Q1 at 60, median at 67, Q3 at 71, maximum at 75. The bottom box plot is labeled October. Minimum at 45, Q1 at 50, median at 60, Q3 at 75, maximum at 85.

What can you tell about the means for these two months?
A. The mean for April is higher than October's mean.
B. There is no way of telling what the means are.
C. The low median for October pulls its mean below April's mean.
D. The high range for October pulls its mean above April's mean./

Answer 1

There is no way of telling what the means are.

Explanation:

I took the test and got it right

Answer 2

The data for April is negatively skewed, hence, most possibly the mean of the distribution is less than the median which is, 67.

The data for October is positively skewed, hence, most possibly the mean of the distribution is greater than the median which is, 60.

But, there is possibility for otherwise also in both of the cases, so there is actually no way of predicting what the actual means are.

Explanation:

The Bowley's measure of skewness for the data on the box-plot showing average daily temperatures in April for a U. S. city is given by,

`\frac {Q_(3) + Q_(1) - 2Q_(2)}{Q_(3) - Q_(1)}`

=
`\frac {71 + 60 - 2 * 67}{71 - 60}`

=
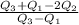
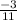`\frac {- 3}{11}` < 0

Hence, the data is negatively skewed, hence, most possibly the mean of the distribution is less than the median which is, 67.

The Bowley's measure of skewness for the data on the box-plot showing average daily temperatures in October for a U. S. city is given by,

`\frac {Q_(3) + Q_(1) - 2Q_(2)}{Q_(3) - Q_(1)}`

=
`\frac {75 + 50 - 2 * 60}{75 - 50}`

=
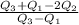
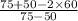
`0.2` > 0

Hence, the data is positively skewed, hence, most possibly the mean of the distribution is greater than the median which is, 60.