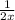Question

Differentiating a Logarithmic Function In Exercise, find the derivative of the function.

y = In (x)^1/2

Answer 1

`(1)/(2x)`

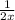
Explanation:

chain rule is used to find a derivativeof a function if the function is a composition of two functions.

The derivative can be found f'(x)= z'(g(x))g'(x) when f(x)=z(g(x)) as

here z(x)=ln(x) and g(x) = x^1/2

If we apply chain rule to y=In (x)^1/2

y'=ln(u)' × ((x)^1/2)' where u=x^1/2

=
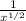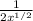
`(1)/(x^(1/2) )` ×
`(1)/(2x^(1/2))`

=
`(1)/(2x)`