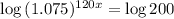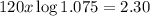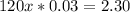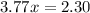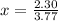Question

Solving Exponential and Logarithmic Equations In Exercise, solve for x.

500(1.075)120x = 100.000

Answer 1

The solution is:

`x = 0.61`

Explanation:

The first step to solve this equation is placing everything with the exponential to one side of the equality, and everything without the exponential to the other side. So

`500(1.075)^(120x) = 100000`

`(1.075)^(120x) = (100000)/(500)`

`(1.075)^(120x) = 200`

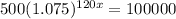
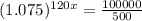
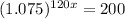
To find x, we have to apply log to both sides of the equality.

We also have that:

`\log{a^(x)} = x\log{a}`

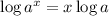
So

`\log{(1.075)^(120x)} = \log{200}`

`120x\log{1.075} = 2.30`

`120x*0.03 = 2.30`

`3.77x = 2.30`

`x = (2.30)/(3.77)`

`x = 0.61`