We can use two properties to solve:
Quotient Rule:
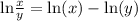
Power Rule:
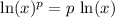
Simplify the expression using the power rule:
In(x - 1/x + 1)^2 → 2 ln (x - 1/x + 1)
Simplify using the quotient rule:
2 ln (x - 1/x + 1) → 2[ln(x - 1) - ln(x + 1)]
Therefore, the the simplified logarithm is 2[ln(x - 1) - ln(x + 1)]
Best of Luck!