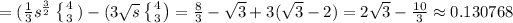Question

Exercise is mixed —some require integration by parts, while others can be integrated by using techniques discussed in the chapter on Integration.

∫^1_0 x^3/√3+x^2 dx.

Answer 1

`\int\limits^1_0 {(x^(3) )/(√(3+x^2) ) } \, dx \approx 0.130768`

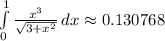
Explanation:

Use Integration by Substitution:

For the integrand
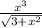`(x^(3) )/(√(3+x^2) )` , substitute:

`u=x^2 \\du=2xdx`

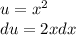
Also, remember to evaluate the new integration limits:

Lower limit:

`u=0^2=0`

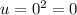
Upper limit:

`u=1^2=1`

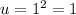
So:

`=(1)/(2) \int\limits^1_0 {(u)/(√(u+3) ) } \, du`

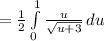
Now, do a new substitution for the integrand
`(u)/(√(u+3) )` :

`s=u+3\\ds=du`

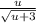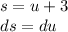
Again, this gives us a new lower limit and a new upper limit:

Lower limit:

`s=0+3=3`

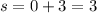
Upper limit:

`s=1+3=4`

`=(1)/(2) \int\limits^4_3 {(s-3)/(√(s) ) } \, ds`

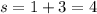
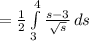
Express
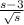`(s-3)/(√(s) )` as
`√(s) - (3)/(√(s) )`

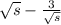
Now, integrate the sum term by term and factor out constants:

`=(1)/(2) \int\limits^4_3 {√(s) } \, ds  - (3)/(2)  \int\limits^4_3 {(1)/(√(s) ) } \, ds`

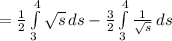
Finally, apply the fundamental theorem of calculus:

`=((1)/(3) s^{(3)/(2)  } \left \{ {{4} \atop {3}} \right. ) - (3√(s) \left \{ {{4} \atop {3}} \right )=(8)/(3) -√(3) +3(√(3) -2)=2√(3) - (10)/(3) \approx0.130768`