Answer:
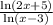 = 0
= 0
Explanation:
Data provided in the question:
In(2x + 5) = In(x - 3)
we can rearrange the above equation as
⇒ In(2x + 5) - In(x - 3) = 0
now,
from the properties of natural log function, we know that
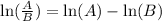
therefore,
we get
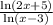 = 0
= 0
Hence,
Expression as the logarithm of a single quantity is
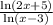 = 0
= 0