Question

Expanding Logarithmic Expressions In Exercise, use the properties of logarithms to rewrite the expression as the sum, difference, or multiple of logarithms.

In x^2/x^2 + 1

Answer 1

`\\ ln(x^2) - ln(x^2 + 1)`.

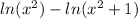For values of x>0, it can be rewritten as
`\\ 2ln(x) - ln(x^2 + 1).`

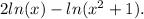
Explanation:

For the expression:

`\\ ln((x^2)/(x^2 + 1))`

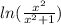
We can apply this logarithmical property:
`\\ ln((x)/(y)) = ln(x) - ln(y).`

Then,

`\\ (x^2)/(x^2 + 1) = ln(x^2) - ln(x^2 + 1).`

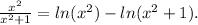
If we assume values of x > 0 (non negative values for x), then the expression could be rewritten as follows:

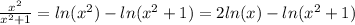`\\ (x^2)/(x^2 + 1) = ln(x^2) - ln(x^2 + 1) = 2 ln(x) - ln(x^2 + 1)`, since
`\\ ln(x^(n)) = n*ln(x).`

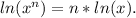
We have to remember that domain (all possible values x) for logarithmic function is for all x > 0, or mathematically expressed as:

Domain:
`\\ x`