Question

Logarithmic and Exponential Forms of Equations In Exercise, write the logarithmic equation as an exponential equation, or vice versa.

e - 4 = 0.0183 ...

Answer 1

Answer : The logarithmic equation of given exponential equation is,
`\ln (0.0183)=-4`

Step-by-step explanation :

As we are given the exponential equation.

`e^(-4)=0.0183`

Formula used :

The inverse property of logarithm for the expression
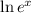`\ln e^x` is:

`\ln e^x=x`

Now we have to determine the logarithmic equation of given exponential equation.

`e^(-4)=0.0183`

Taking natural logarithm both sides as,

`\ln e^(-4)=\ln (0.0183)`

`-4=\ln (0.0183)`

`\ln (0.0183)=-4`

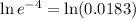
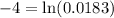
Thus, the logarithmic equation of given exponential equation is,
`\ln (0.0183)=-4`