Question

Logarithmic and Exponential Forms of Equations In Exercise, write the logarithmic equation as an exponential equation, or vice versa.

In 12 = 2.4849...

Answer 1

`12 = e^(2.4849)`

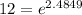
Explanation:

For this case we have the following expression:

`ln(12) = 2.4849`

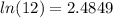
We need to remember that the natural log and the exponentiation with the base the euler number e are inverse operations, and if we apply exponentiation on both sides of the equation we got this:

`e^(ln(12)) = e^(2.4849)`

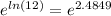
We have the identity operator for this
`e^(ln(x))= x`

`12 = e^(2.4849)`

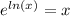
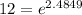
And that would be our final answer for this case.