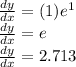Question

Finding an Equation of a Tangent Line In Exercise, find an equation of the tangent line to the graph of the function at the given point.

y = xe^x - e^x, (1, 0)

Answer 1

Equation of tangent:

`y = xe^(x)`

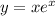
At point (1,0):

y = 2.713

Explanation:

The equation of tangent line to the function can be calculated by taking the first derivative.

We have,

`y = xe^(x)-e^(x)\\(dy)/(dx)=(d)/(dx)[ xe^(x) ]-(d)/(dx) [e^(x)]\\`

Applying Product Rule:

d/dx [u.v] = (d/dx u) . (v) + (u) . (d/dx v)

Therefore,

`(dy)/(dx)=(d)/(dx)(x) . e^(x)+x .(d)/(dx)(e^(x))- (d)/(dx)(e^(x))\\\\(dy)/(dx)=(1)(e^(x))+(x)(e^(x))-e^(x)\\ (dy)/(dx)=xe^(x)\\\\`

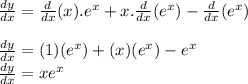
The above equation is the equation of tangent line.

The point given is (1,0):

So,

`(dy)/(dx) = (1)e^(1)\\ (dy)/(dx) = e\\(dy)/(dx) = 2.713`