Answer:
We can say that is FALSE because the inhomogeneous sytem
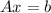 can present an unique solution
can present an unique solution
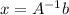 if
if
 , so this is a good counter example on which we have a vctor that is not the trivial solution and we don't have an infinite number of solution.
, so this is a good counter example on which we have a vctor that is not the trivial solution and we don't have an infinite number of solution.
Explanation:
For this case we can use the following definition:
Let
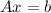 a linear system, this system is called homogeneous if
a linear system, this system is called homogeneous if
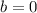 and in other case is called inhomogeneous.
and in other case is called inhomogeneous.
So then for the statement "The inhomogeneous system of equations Ax=b, where
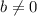 , has either the trivial solution or an infinite number of the solutions."
, has either the trivial solution or an infinite number of the solutions."
We can say that is FALSE because the inhomogeneous sytem
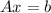 can present an unique solution
can present an unique solution
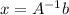 if
if
 , so this is a good counter example on which we have a vctor that is not the trivial solution and we don't have an infinite number of solution.
, so this is a good counter example on which we have a vctor that is not the trivial solution and we don't have an infinite number of solution.