Question

Profit The net profits P (in millions of dollars) of Medco Health solutions from 2000 through 2009 are shown in the table.

Year 2000 2001 2002 2003 2004
Profit 216.8 256.6 361.6 425.8 481.6
Year 2005 2006 2007 2008 2009
Profit 602.0 729.8 912.0 1102.9 1280.3
A model for this data is given by p = 223.89e01979t, where t represents the year, with t = 0 corresponding to 2000.
(a) How well does the model fit the data?
(b) Find a linear model for the data. How well does the linear model fit the data? Which model, exponential or linear, is a better fit?
(c) Use both models to predict the net profit in 2015.

Answer 1

a) For this case we have the linear model given:

`P(t) = 223.89 e^(0.1979t)`

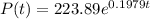
And we want to see the fit to the model so we can calculate the value for the model and the difference respect to the observed value.

`t=0, P(0)= 223.89 e^(0.1979*0)= 223.89 , e= |216.8-223.89|=7.09`

`t=1, P(1)= 223.89 e^(0.1979*1)= 272.89 , e= |256.6-272.89|=16.29`

`t=2, P(2)= 223.89 e^(0.1979*2)=332.60  , e= |361.6-332.60|=29.00`

`t=3, P(3)= 223.89 e^(0.1979*3)= 405.39 , e= |425.8-405.39|=20.41`

`t=4, P(4)= 223.89 e^(0.1979*4)= 494.11 , e= |481.6-494.11|=12.51`

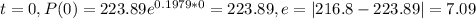
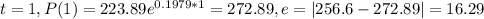
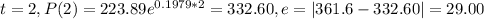
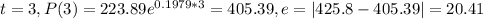
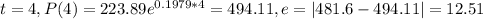
As we can see the model not perfect fits to the data but the residuals are not to higher compared to the real values.

b)
`y=116.85 x +111.15`

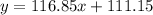
c)
`t=15, P(15)= 223.89 e^(0.1979*15)= 4357.505`

`y=116.85(15) +111.15=1863.9`

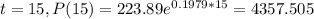
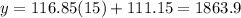
As we can see the difference between the two models is higher.

Explanation:

For this case we have the following data:

x=t y=P(t)

0 216.8

1 256.6

2 361.6

3 425.8

4 481.6

5 602.0

6 729.8

7 912.0

8 1102.9

9 1280.3

Where x represent the year, with t = 0 corresponding to 2000

Part a

For this case we have the linear model given:

`P(t) = 223.89 e^(0.1979t)`

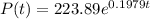
And we want to see the fit to the model so we can calculate the value for the model and the difference respect to the observed value.

`t=0, P(0)= 223.89 e^(0.1979*0)= 223.89 , e= |216.8-223.89|=7.09`

`t=1, P(1)= 223.89 e^(0.1979*1)= 272.89 , e= |256.6-272.89|=16.29`

`t=2, P(2)= 223.89 e^(0.1979*2)=332.60  , e= |361.6-332.60|=29.00`

`t=3, P(3)= 223.89 e^(0.1979*3)= 405.39 , e= |425.8-405.39|=20.41`

`t=4, P(4)= 223.89 e^(0.1979*4)= 494.11 , e= |481.6-494.11|=12.51`

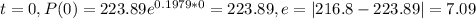
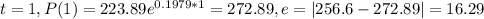
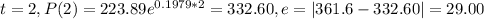
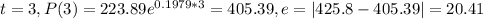
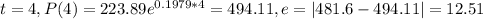
As we can see the model not perfect fits to the data but the residuals are not to higher compared to the real values.

Part b

For this case we need to calculate the slope with the following formula:

`m=(S_(xy))/(S_(xx))`

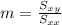
Where:

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)`

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)`

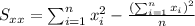
So we can find the sums like this:

`\sum_(i=1)^n x_i =45`

`\sum_(i=1)^n y_i =6369.4`

`\sum_(i=1)^n x^2_i =285`

`\sum_(i=1)^n y^2_i =5239157`

`\sum_(i=1)^n x_i y_i =38302.3`

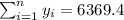
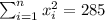
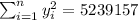
With these we can find the sums:

`S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=285-(45^2)/(10)=82.5`

`S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)=38302.3-(45*6369.4)/(10)=964-`

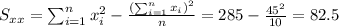
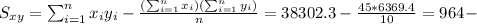
And the slope would be:

`m=(9640)/(82.5)=116.85`

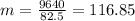
Nowe we can find the means for x and y like this:

`\bar x= (\sum x_i)/(n)=(45)/(10)=4.5`

`\bar y= (\sum y_i)/(n)=(6369.4)/(10)=636.94`

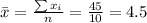
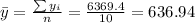
And we can find the intercept using this:

`b=\bar y -m \bar x=636.94-(116.85*4.5)=111.15`

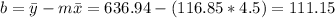
So the line would be given by:

`y=116.85 x +111.15`

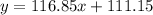
Part c

`t=15, P(15)= 223.89 e^(0.1979*15)= 4357.505`

`y=116.85(15) +111.15=1863.9`

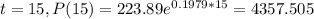
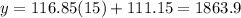
As we can see the difference between the two models is higher.