Question

Demand The demand function for a product is modeled by

p = 8000(1 - 5/5 + e-0.002x).
Find the price p (in dollars) of the product when the quantity demanded is (a) x = 1000 units and (b) x = 2500 units, (c) what is the limit of price as x increases without bound?

Answer 1

a) 210.8 b) 10.77 c) 0

Explanation:

a)p = 8000(1 - 5/5 + e^-0.002x).

when x = 1000 units

p = 8000 ( 1 - (5 / (5 + e ^(-0.002 × 1000)))= 210.8

b) when x = 2500

p = 8000 ( 1 - (5/(5 + e ^(-0.002 × 2500)))

p = 10.77

c) [/tex]
`\lim_(x \to \infty) p`

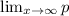
p = 8000 ( 1 - (5/(5+ e^(-0.002∞)))

p = 8000 ( 1 - (5 / (5+ e^-∞))

e^-∞ = 0

p =8000( 1- (5/5))

p = 8000 (1-1) = 0

the limit of price as x increase without bound reduces to zero