Question

Use integration by parts to find the integrals in Exercise.
∫^2_1 ln 5x dx.

Answer 1

`\int^2_1 ln 5x dx=1.99`

Explanation:

we have the integral:

`\int^2_1 ln 5x dx`

The formula to integrate by parts is:

`\int udv=uv-\int vdu`

in this case we will use
`u=ln5x` and
`dv=dx`.

so
`v=x`

and using logarithm derivation
`d(lnw)=(dw)/(w)`

`du=(5)/(5x) =(1)/(x)`

thus:

`\int ln 5x dx=(ln5x)(x)- \int x((1)/(x))dx`

`\int ln 5x dx=xln5x - \int dx`

`\int ln 5x dx=xln5x - x`

evaluating the limits:

`\int^2_1 ln 5x dx=[xln5x - x]^2_1\\=[2ln(5*2)- 2]-[1ln(5*1) - 1]\\=[2ln10-2]-[ln5-1]\\=[2(2.3)-2]-[1.61-1]\\=[4.6-2]-0.61\\=2.6-0.61\\=1.99`

Answer 2

`\displaystyle \int\limits^2_1 {\ln 5x} \, dx = \ln(20) - 1`

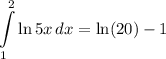
General Formulas and Concepts:

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Integration

• Integrals

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

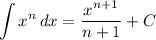
Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

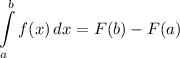
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

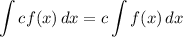
Integration by Parts:
`\displaystyle \int {u} \, dv = uv - \int {v} \, du`

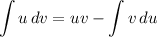
• [IBP] LIPET: Logs, inverses, Polynomials, Exponentials, Trig

Explanation:

Step 1: Define

Identify

`\displaystyle \int\limits^2_1 {\ln 5x} \, dx`

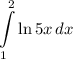
Step 2: Integrate Pt. 1

Identify variables for integration by parts using LIPET.

1. Set u:
   `\displaystyle u = \ln 5x`
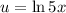
2. [u] Logarithmic Differentiation [Derivative Rule - Chain Rule]:
   `\displaystyle du = ((5x)')/(5x) \ dx`
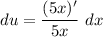
3. [du] Basic Power Rule [Derivative Rule - Multiplied Constant]:
   `\displaystyle du = (5)/(5x) \ dx`
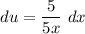
4. [du] Simplify:
   `\displaystyle du = (1)/(x) \ dx`
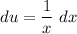
5. Set dv:
   `\displaystyle dv = dx`
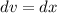
6. [dv] Integration Rule [Reverse Power Rule]:
   `\displaystyle v = x`

Step 3: Integrate Pt. 2

1. [Integral] Integration by Parts:
   `\displaystyle \int\limits^2_1 {\ln 5x} \, dx = x \ln(5x) \bigg| \limits^2_1 - \int\limits^2_1 {} \, dx`
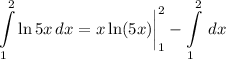
2. [Integral] Integration Rule [Reverse Power Rule]:
   `\displaystyle \int\limits^2_1 {\ln 5x} \, dx = x \ln(5x) \bigg| \limits^2_1 - x \bigg| \limits^2_1`
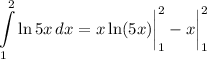
3. Evaluate [Integration Rule - Fundamental Theorem of Calculus 1]:
   `\displaystyle \int\limits^2_1 {\ln 5x} \, dx = \ln(20) - 1`

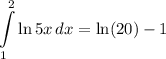
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration