Question

Differentiating Exponential Functions In Exercise, find the derivative of the function.

y = 4e(x)^1/2

Answer 1

Answer:
`\frac{2e^{x^(1)/(2)}}{√(x)}` .

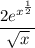Explanation:

Properties of derivative :

• 
  `(d)/(dx)(e^x)=e^x`
• 
  `(d)/(dx)(x^n)=x^(n-1)` (1)
• 
  `(d)/(dx)(ax)=a`

• Let g be a differentiable function , then
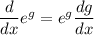  `(d)/(dx)e^g=e^g(dg)/(dx)` (2)

Given function :
`y = 4e^{x^{(1)/(2)}}`

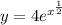
Now , differentiate both sides of the above equation with respect to x , we get

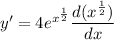`y'=4e^{x^(1)/(2)}\frac{d(x^{(1)/(2)})}{dx}` (Using(2))

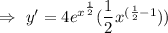`\Rightarrow\ y'=4e^{x^(1)/(2)}((1)/(2)x^{((1)/(2)-1}))` (Using (1))

`\Rightarrow\ y'=2e^{x^(1)/(2)}x^{-(1)/(2)}`

`\Rightarrow\ y'=\frac{2e^{x^(1)/(2)}}{√(x)}`

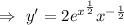
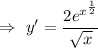
Hence, the derivative of the given function is
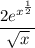`\frac{2e^{x^(1)/(2)}}{√(x)}` .