Answer:
8.733046.
Explanation:
We have been given a definite integral
 . We are asked to find the value of the given integral using integration by parts.
. We are asked to find the value of the given integral using integration by parts.
Using sum rule of integrals, we will get:
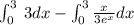
We will use Integration by parts formula to solve our given problem.
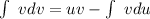
Let
 and
and
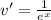 .
.
Now, we need to find du and v using these values as shown below:
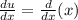
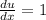


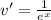
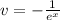
Substituting our given values in integration by parts formula, we will get:

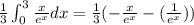
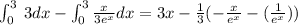
Compute the boundaries:
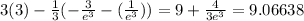
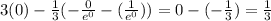
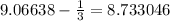
Therefore, the value of the given integral would be 8.733046.