Question

An airplane capable of an airspeed of 100 km/hr is 60 km off the coast above the sea. If the wind is blowing from the coast out to sea at 40 km/hr, what is the least amount of time it will take for the plane to get to shore ?

Answer 1

To solve this problem we will apply the concepts related to relative speed. We will obtain it from the deduction made on the aircraft as a speed of the two components that act on it. Through the kinematic equations of motion, we can then calculate the time required.

The airspeed of airplane is 100km/h while the wind is blowing from the coast out to sea at 40km/h. Wind is blowing from the coast out to sea means that it opposes the airspeed. Therefore, resultant relative speed of airplane is

`v_r = 100-40=60km/h`

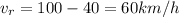
Total distance is 60km then with this net velocity we have that the required time is

`v = (x)/(t) \rightarrow t = (x)/(v)`

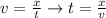
Where,

x = Displacement

t = Time

v = Velocity

Replacing,

`t = (60km)/(60km/h) = 1hour`

`t = 60 minutes`

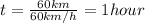
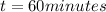
Therefore the time taken by the plane to reach the shore is 60 minutes