Answer:
Upon multiplication with this matrix A, it gives a vector perpendicular to the original, with a magnitude of
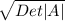 times of the original.
times of the original.
If a 2x2 matrix A has complex eigenvalues, this is an antisymmetric matrix.
Therefore:
![A=\left[\begin{array}{cc}0&a\\-a&0\end{array}\right] \\Det|A|=a^2](https://img.qammunity.org/2021/formulas/mathematics/college/9kcrelli0fc8gdlfur4nnpjf1yiy5xzoj3.png)
if we multiply (x,y) to this matrix A:
^T=(ay,-ax)^T=√(Det|A|) (y,-x)^T](https://img.qammunity.org/2021/formulas/mathematics/college/slohl3fqhiid00oek2cu6qy2he0dyhcsq7.png)