Answer:
(a) annually = 17.67 years
(b) monthly = 17.36 years
(c) daily = 17.34 years
(d) continuously = 17.328 years
Explanation:
given data
principal = $500
annual rate = 4%
solution
we know here amount formula that is
amount = principal ×
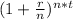 ..................1
..................1
put here value for compound annually
1000 = 500 ×

take ln both side
ln 2 = ln
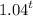
t = 17.67 years
and
put value now in equation 1 for monthly
amount = principal ×
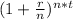
1000 = 500 ×
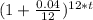
take ln both side
ln 2 = 12t × ln(1.003333)
t = 17.36 years
and
put value now in equation 1 for daily
amount = principal ×
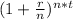
1000 = 500 ×
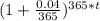
take ln both side
ln 2 = 365 t × ln (1.0001095)
t = 17.34 years
and
for compound continuously
amount = principal ×
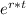 .................2
.................2
put here value
1000 = 500 ×
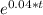
t = 17.328 years