Answer:
For n=1
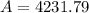
For n=2
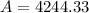
For n=4
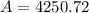
For n=12
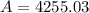
For n=365
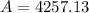
Using exponential function
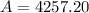
Explanation:
P=$3000
r = 3.5%
t = 10 years
we need to find accumulated Amount A for n= 1, 2, 4, 12 and 365
As we know, continuous compounding can be found by
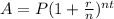
Where P is the invested amount with interest rate r for t years
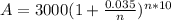
For n=1
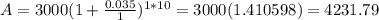
For n=2
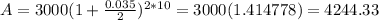
For n=4
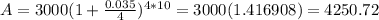
For n=12
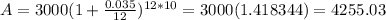
For n=365
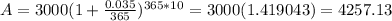
As the value of n increases, the change in the value of A decreases and eventually for very large value of n, A becomes constant and doesnt change anymore.
This is why we also use exponential function for continuous compounding
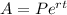
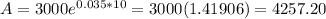
Hence we got same result with above equation and proved that exponential function provides accurate results for very large value of n.