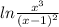Answer:
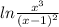
Explanation:
We have given expression
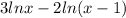
According to logarithmic property

Now again using logarithmic property when two log function are subtracted with each other then their functions are divide by each other
So
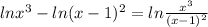
So by using logarithmic property and after solving answer will be