Question

An airplane travels 460 miles from San Diego to San Francisco in 2.5 hours, going against the wind. The return trip is with the wind, and takes only 2 hours. Find the rate of the airplane with no wind. Find the rate of the wind.

Answer 1

The airplane flies at 207 mi/h with no wind. The rate of the wind is 23 mi/h.

Answer 2

The speed of airplane is 207 miles per hour

The speed of wind is 23 miles per hour

Explanation:

Given as :

The distance cover by airplane against the wind = D = 460 miles

The time taken to cover D distance = T = 2.5 hours

Again

The distance cover by airplane with the wind = d = 460 miles

The time taken to cover d distance = t = 2 hours

Let The speed of airplane = x mile per hour

Let The speed of wind = y miles per hour

According to question

∵ Speed =
`(\textrm Distance)/(\textrm Time)`

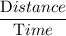
For Against the wind

x - y =
`(\textrm D)/(\textrm T)`

Or, x - y =
`(\textrm 460 miles)/(\textrm 2.5 hours)`

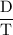
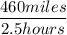
Or, x - y = 184 mph ........1

For with the wind

x + y =
`(\textrm d)/(\textrm t)`

Or, x + y =
`(\textrm 460 miles)/(\textrm 2 hours)`

Or, x + y = 230 mph ........2

Now, Solving eq 1 and eq 2

(x - y) + (x + y) = 184 mph + 230 mph

Or, (x + x) + ( - y + y) = 414 mph

Or, 2 x + 0 = 414 mph

∴ x =
`(414)/(2)`

i,e x = 207 mph

So, The speed of airplane = x = 207 miles per hour

Now, Put the value of x into eq 1

∵ x - y = 184 mph

So, 207 mph - y = 184 mph

Or, y = 207 mph - 184 mph

i.e y = 23 mph

So, The speed of wind = y = 23 miles per hour

Hence, The speed of airplane is 207 miles per hour and The speed of wind is 23 miles per hour . Answer