Question

The formula T= 2pi sqrt(L/32) relates the time, T, in seconds for a pendulum with the length, L, in feet, to make one full swing back and forth. What is the length of a pendulum that makes one full swing in 1.75 seconds? Use 3.14 for pi.

Answer 1

B. 4 feet.

Explanation:

Just did the Unit Test Review on Edg (2020-2021)!!

Answer 2

The length of pendulum is 2.485 feet

Solution:

Given that,

The formula T= 2pi sqrt(L/32) relates the time, T, in seconds for a pendulum with the length, L, in feet, to make one full swing back and forth

Therefore, the given formula is:

`T=2\pi \sqrt{(L)/(32) }`

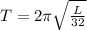
We have to find the length of pendulum that makes one full swing in 1.75 seconds

So the modify the given equation to find "L"

`T=2\pi \sqrt{(L)/(32) }\\\\ \sqrt{(L)/(32) }=(T)/(2 \pi)\\\\\text{Taking square root on both sides }\\\\(L)/(32) = (T^2)/(4 \pi^2)\\\\L = (T^2)/(4 \pi^2) * 32\\\\L = (T^2)/(\pi^2 ) * 8`

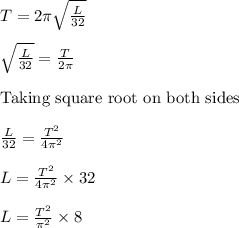
Substitute T = 1.75 seconds and
`\pi = 3.14`

`L = (1.75^2)/(3.14 * 3.14) * 8\\\\L = (3.0625)/(9.8596) * 8\\\\L = 2.485`

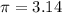
Thus length of pendulum is 2.485 feet approximately