Question

The remainder when p\left(x\right)=x^3-2x^2+8x+kp ( x ) = x 3 − 2 x 2 + 8 x + k by (x-2) is 19. What is the remainder when p(x) is divided by (x+2)?

Answer 1

✩ Given Polynomial : x³ - 2x² + 8x + k

when p(x) is divided by (x - 2) it gives 19 as remainder. HENCE WE CAN SAY.

⠀

`:\implies\sf p(x)=x^3-2x^2+8x+k\\\\\\:\implies\sf p(x-2=0)=x^3-2x^2+8x+k\\\\\\:\implies\sf p(x=2)=x^3-2x^2+8x+k\\\\\\:\implies\sf p(2)=(2)^3-2(2)^2+8(2)+k\\\\\\:\implies\sf 19 = 8 - 8 + 16 + k\\\\\\:\implies\sf 19 - 16 = k\\\\\\:\implies\sf k = 3`

`\rule{150}{1}`

☯
`\underline{\boldsymbol{According\: to \:the\: Question\:now :}}`

`:\implies\sf p(x)=x^3-2x^2+8x+k\\\\\\:\implies\sf p(x+2=0)=x^3-2x^2+8x+k\\\\\\:\implies\sf p(x=-\:2)=x^3-2x^2+8x+k\\\\\\:\implies\sf p(-\:2)=(-\:2)^3-2(-\:2)^2+8(-\:2)+3\\\\\\:\implies\sf p(-\:2) = - \:8 - \:8 - \:16 + 3\\\\\\:\implies\underline{\boxed{\sf p(-\:2) = - \:29}}`

⠀

`\therefore\:\underline{\textsf{Hence, required remainder will be \textbf{- 29}}}.`

Answer 2

Remainder when p(x) is divided by (x+2) is -29

Explanation:

p(x) =
`x^(3) - 2x^(2) + 8x + k`

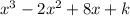
When p(x) is divided by (x-2), remainder is 19.

p(x - 2 = 0) gives the remainder when p(x) is divided by (x-2)

x - 2 = 0

x = 2

p(x-2=0) = p(2) =
`2^(3) - 2(2^(2)) + 8(2) + k` = 19

8 - 8 + 16 + k = 19

k = 3

p(x) =
`x^(3) - 2x^(2) + 8x + 3`

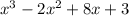
p(x + 2 = 0) gives the remainder when p(x) is divided by (x+2)

x + 2 = 0

x = -2

p(x+2=0) = p(-2) =
`(-2)^(3) - 2((-2)^(2)) + 8(-2) + 3`

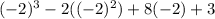
p(-2) = - 8 - 8 - 16 + 3 = -29

Remainder when p(x) is divided by (x+2) is -29