The solution to given system of equations y = 3x - 9 and y = -2x + 16 are (x, y) = (5, 6)
The solution to given system of equations y = 5x + 22 and -6x - 4y = -10 are (x, y) = (-3, 7)
Solution:
Given that, we have to solve each system by substitution method
Given system of equations are:
y = 3x - 9 ----------- eqn 1
y = -2x + 16 -------- eqn 2
Substitution method is done by substituting eqn 2 in eqn 1
Substitute the value of "y" from eqn 2 into eqn 1
-2x + 16 = 3x - 9
Move the variables to one side and constants to other side
-2x - 3x = -9 - 16
Combine the like terms
-5x = -25
Cancel the negative sign on both sides of equation
5x = 25
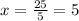
x = 5
Substitute x = 5 in eqn 1
y = 3(5) - 9
y = 15 - 9
y = 6
Thus solution to given system of equations are (x, y) = (5, 6)
Given another system of equations are:
y = 5x + 22 ----- eqn 1
-6x - 4y = -10 ------ eqn 2
Substitute eqn 1 in eqn 2
-6x - 4(5x + 22) = -10
-6x - 20x - 88 = -10
Move the variables to one side and constants to other side
-26x = -10 + 88
-26x = 78
x = -3
Substitute x = -3 in eqn 1
y = 5( - 3) + 22
y = -15 + 22
y = 7
Thus solution to given system of equations are (x, y) = (-3, 7)