Question

Find two unit vectos that are orthogonal to both [0,1,2] and [1,-2,3]

Answer 1

Let the vectors be

a = [0, 1, 2] and

b = [1, -2, 3]

( 1 ) The cross product of a and b (a x b) is the vector that is perpendicular (orthogonal) to a and b.

Let the cross product be another vector c.

To find the cross product (c) of a and b, we have

`\left[\begin{array}{ccc}i&j&k\\0&1&2\\1&-2&3\end{array}\right]`

c = i(3 + 4) - j(0 - 2) + k(0 - 1)

c = 7i + 2j - k

c = [7, 2, -1]

( 2 ) Convert the orthogonal vector (c) to a unit vector using the formula:

c / | c |

Where | c | = √ (7)² + (2)² + (-1)² = 3√6

Therefore, the unit vector is

`([7,2,-1])/(3√(6) )`

or

[
`(7)/(3√(6) )` ,
`(2)/(3√(6) )` ,
`(-1)/(3√(6) )` ]

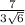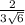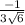The other unit vector which is also orthogonal to a and b is calculated by multiplying the first unit vector by -1. The result is as follows:

[
`(-7)/(3√(6) )` ,
`(-2)/(3√(6) )` ,
`(1)/(3√(6) )` ]

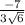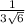In conclusion, the two unit vectors are;

[
`(7)/(3√(6) )` ,
`(2)/(3√(6) )` ,
`(-1)/(3√(6) )` ]

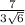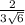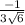and

[
`(-7)/(3√(6) )` ,
`(-2)/(3√(6) )` ,
`(1)/(3√(6) )` ]

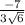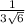Hope this helps!