Question

Find the value of the integral that converges.
∫^0_-[infinity] x/x^2+3 dx.

Answer 1

Integral doesn't converge

Explanation:

In order to computed the improper integral replace infinite limit with a finite value:

`\lim_k \to -\infty} (\int\limits^0_k {(x)/(x^2+3) } \, dx  )`

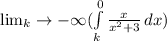
For the integrand
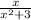`(x)/(x^2+3)` substitute:

`u=x^2+3\\du=2xdx`

`\lim_k \to -\infty} ((1)/(2)  \int\limits^0_k {(1)/(u) } \, du  )`

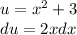
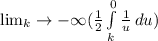
The integral of 1/u is log(u):

Applying the fundamental theorem of calculus and substituing back for u=x^2 +3:

`\lim_(k \to -\infty) ((1)/(2) log(x^2+3) \left \{ {{0} \atop {k}} \right )`

Evaluating the limits:

`\lim_(k \to -\infty) ((1)/(2) log(x^2+3) \left \{ {{0} \atop {k}} \right ) =0.549-\infty= \infty`

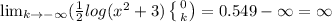
Hence, the integral doesn't converge