Question

Find the value of the integral that converges.
∫^[infinity]_0 dx/(3x+1)^2.

Answer 1

The given integral is convergent and its value is
`(1)/(3)`.

Explanation:

We have been given a definite integral
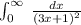`\int _0^(\infty )\:(dx)/(\left(3x+1\right)^2)`. We are asked to determine whether the given integral converges or diverges.

We will use u-substitution to solve our given integral as:

Let
`u=3x+1`.

`(du)/(dx)=3`

`dx=(1)/(3)du`

`\int _0^(\infty )\:(dx)/(\left(3x+1\right)^2)=\int _0^(\infty )\:(1)/(\left(u\right)^2)*(1)/(3)du`

`\int _0^(\infty )\:(dx)/(\left(3x+1\right)^2)=(1)/(3)\int _0^(\infty )\:(1)/(\left(u\right)^2)du`

`\int _0^(\infty )\:(dx)/(\left(3x+1\right)^2)=(1)/(3)\int _0^(\infty )\:u^(-2)du`

`\int _0^(\infty )\:(dx)/(\left(3x+1\right)^2)=(1)/(3)*(u^(-2+1))/(-2+1)`

`\int _0^(\infty )\:(dx)/(\left(3x+1\right)^2)=(1)/(3)*(u^(-1))/(-1)=-(1)/(3u)=-(1)/(3(3x+1))`

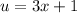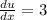
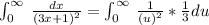
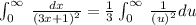
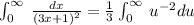
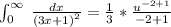
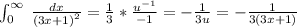
Now, we will compute the boundaries as:

`-(1)/(3(3(\infty)+1))=-(1)/(\infty)=0`

`-(1)/(3(3(0)+1))=-(1)/(3(1))=-(1)/(3)`

`0-(-(1)/(3))=(1)/(3)`

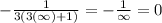
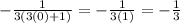
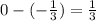
Therefore, the given integral is convergent and its value is
`(1)/(3)`.