Question

If a is a vector and c is a scalar, how is ca related to a gemotrically? How do you find ca algebraically?

Answer 1

Geometrically, ca is an extension or contraction of a, and algebraically is a multiplication of c times every coordinate of a.

Explanation:

A vector is an element of a vectorial space which could have n-coordinates (or dimensions). A scalar is just a number (they don't specify if it is real, complex, rational, etc.).

In order to find ca (or c*a), we have that, in general

`a=(x_(1),x_(2),...,x_(n))`

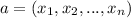
is the vector a, and ca is c times the vector a

`ca=(x_(1),x_(2),...,x_(n))=(cx_(1),cx_(2),...,cx_(n))`

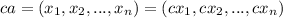
Geometrically, this represents an extension or contraction of the vector a.