Question

Find the equation of the sphere that passes through the point (6,-2,3) and has centre (-1,2,1).

(b) Find the curve in which this sphere intersects the yz-plane
(c) Find the center and radius of the sphere
x^2 + y^2 + z^2 - 8x + 2y+ 6z+1=0

Answer 1

a) The sphere has radius equal to the distance between the center and the given point:

`√((6+1)^2+(-2-2)^2+(3-1)^2)=√(69)`

So the sphere has equation

`(x-6)^2+(y+2)^2+(z-3)^2=69`

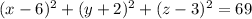
b) The sphere intersects the
`y`-
`z` plane whenever
`x=0`:

`(-6)^2+(y+2)^2+(z-3)^2=69\implies(y+2)^2+(z-3)^2=33`

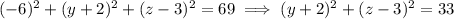
which is the equation of the circle centered at (-2, 3) with radius
`√(33)`.

c) Complete the squares:

`x^2+y^2+z^2-8x+2y+6z+1=0`

`(x^2-8x+16)+(y^2+2y+1)+(z^2+6z+9)+1=16+1+9`

`(x-4)^2+(y+1)^2+(z+3)^2=25`

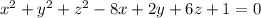
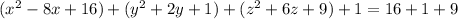
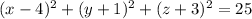
So this sphere has radius 5 and is centered at (4, -1, -3).