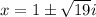Question

Limited time . 10 points

Answer 1

Therefore the value of x is

`x=1\pm√(19)i`

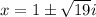
Explanation:

Given:

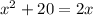`x^(2)+20=2x` which is

`x^(2)-2x+20=0`

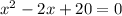
To Find:

x = ? using Quadratic Formula

Solution:

For a Quadratic Equation ax² + bx + c = 0 , Formula Method is given as

`x=\frac{-b\pm\sqrt{b^(2)-4ac}}{2a}`

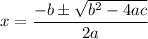
On Comparing with above we get

`a=1\\b=-2\\c=20`

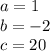
Substituting a , b , c in Formula method we get

`x=\frac{-(-2)\pm\sqrt{(-2)^(2)-4(1)(20)}}{2* 1}\\\\x=(2\pm√(-76))/(2)\\\\x=(2\pm2√(19)i)/(2)\\Dividing\ by\ 2\ we\ get\\\\x=1 \pm√(19)i`

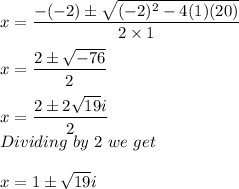
Therefore the value of x is

`x=1\pm√(19)i`