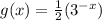Question

Which function represents g(x), a reflection of f(x) = On a coordinate plane, 2 exponential functions are shown. g (x) decreases in quadrant 2 and approaches y = 0 in quadrant 1. It goes through (negative 1, 1) and crosses the y - axis at (0, 0.5).(3)x across the y-axis? g(x) = 2(3)x g(x) = −One-half(3)x g(x) = One-half(3)−x g(x) = 2(3)−x

Answer 1

g(x)=1/2(3^-x)

Answer 2

`g(x)=(1)/(2)(3^(-x))`

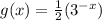
Explanation:

Given:

The graph of function
`f(x)\ and\ g(x)` are given.

The equation for
`f(x)` is given as:

`f(x)=3^x`

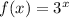
Now, the graph of
`g(x)` is a reflection of
`f(x)`.

The graph of
`g(x)` passes through the point (-1, 1.5) [second quadrant] and crosses the y-axis at (0, 0.5).

As evident from the graph, the functions
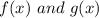`f(x)\ and\ g(x)` are reflections about the y-axis.

We know the transformation rule for reflection about the y-axis as:

`f(x)\to f(-x)\\\\\therefore 3^x\to3^(-x)....(\textrm{Reflection about y-axis})`

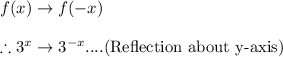
Now, the y-intercept of the function
`y=3^(-x)` is obtained by plugging in
`x=0`. This gives,

`y=3^0=1`

So, the y-intercept is at (0, 1). But the graph of
`g(x)` crosses the y-axis at (0, 0.5). As we observe, the coordinate rule for the transformation can be written as:

(0, 1) → (0, 0.5)

`(x,y)\to (x,(1)/(2)y)`

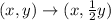
So, the reflected graph is compressed vertically by a factor of
`(1)/(2)`.

Therefore, the transformation is given as:

`y\to (1)/(2)y\\\\\therefore 3^(-x)\to (1)/(2)(3^(-x))`

Therefore, the equation for
`g(x)` is:

`g(x)=(1)/(2)(3^(-x))`