Question

Solve the inequality in terms of intervals and illustrate the solution set on the real number line. (x − 1)(x − 8) > 0

Answer 1

The solution set of the given inequality is (-∞,1) ∪ (8,∞).

Explanation:

The given inequality is

`(x -1)(x -8) > 0`

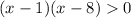
The related equation is

`(x -1)(x -8)=0`

`x=1,8`

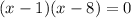
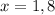
Two numbers 1 and 8 divide the number line in three intervals. (-∞,1), (1,8) ,(8,∞).

Intervals check point (x -1)(x -8) > 0 True or False

(-∞,1) 0 (-1)(-8)=8>0 True

(1,8) 2 (2-1)(2-8)=-6>0 False

(8,∞) 9 (9-1)(9-8)=8>0 True

The given inequality is true for (-∞,1) and (8,∞).

Therefore, the solution set of the given inequality is (-∞,1) ∪ (8,∞).