Question

Describe the type of integral for which integration by parts is useful.

Answer 1

When two functions are multiplied

Explanation:

Integration by parts is useful when there is a product of two functions

for example;∫2xcosxdx

The two functions are 2x and cosx which can not be multiplied if we don't know the values of x.

the functions are represented by u and dv and the integration is calculated as follows.

∫udv = uv - ∫vdu

Answer 2

Two different functions multiplying each other

Explanation:

Integration by part is useful when it comes to these kinds of functions:

`\displaystyle \large{\int x \sin x \ dx}\\\displaystyle \large{\int xe^x \ dx}\\\displaystyle \large{\int e^x \sin x \ dx}`

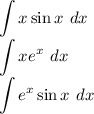
These integrands cannot be integrated normally, you can’t simply just integrate individually since that only applies to addition/subtraction property and they are multiplying.

The by part method is also useful when it comes to integrate a function that does not have their integration formula by default such as:

`\displaystyle \large{\int \ln x \ dx}\\\displaystyle \large{\int \arcsin x \ dx}`

The method is to let u = one function and dv = another function. That means Integration by part can also be called the integration of product rules. The formula of integration by part is:

`\displaystyle \large{\int udv = uv - \int vdu}`

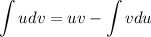
This method has us to substitute u and dv appropriately, that’s why LIATE exists to help you for which function should be u and dv.

LIATE

Stands for Logarithm, Inverse (Trigonometric), Algebraic, Trigonometric, Exponential. LIATE is the order of what should be u first. That means if we are given an integrand of logarithm and trigonometric, we should let u = logarithm and dv = trigonometric.

After letting u and dv, you’ll have to obtain du and v, so you have to differentiate u and integrate dv, which is the reason why logarithm and Inverse trigonometric are both at top because they don’t have integration formula.

After obtaining du and v, you’ll have everything you need and you just simply substitute the terms and evaluate. Here’s the example of by part integration.

`\displaystyle \large{\int x \sin x \ dx}`

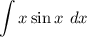
From LIATE, let u = x and dv = sinxdx.

Therefore, du = dx and v = -cosx

Substitute in the formula of by part:

`\displaystyle \large{\int x\sin x \ dx = -x \cos x - \int (-\cos x) \ dx}`

Property/Formulas

`\displaystyle \large{- \int -f(x) \ dx = \int f(x) \ dx}\\\displaystyle \large{\int \sin x \ dx = -\cos x + C}\\\displaystyle \large{\int \cos x \ dx = \sin x + C}`

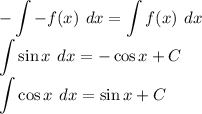
Therefore:

`\displaystyle \large{\int x\sin x \ dx = -x \cos x + \int \cos x \ dx}\\\displaystyle \large{\int x\sin x \ dx = -x \cos x + \sin x + C}`

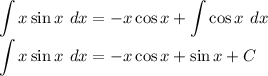
This is the example of integration by part.