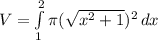Question

Determine whether the statement is true or false, and explain why.

The volume of the solid formed by revolving the function f(x) = √x^2+1 about the x-axis on the interval [1, 2] is given by ∫^2_1π√x^2+1 dx.

Answer 1

The statement is true

Explanation:

Volume of a Solid of revolution:

when a region in the plane is revolved about a given line that is called axis of revolution, then we get a solid of revolution.

In this problem we want to find the volume of a solid formed by revolving the function
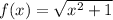`f(x)=\sqrt{x^(2)+1 }` about the x-axis on the interval [1,2]

We can find the volume of any solid by integrating its area

`V=\int\limits^b_a {A} \, dx` eq. 1

where
`A=\pi r^(2)`

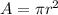
and
`r^(2) =(f(x))^(2) =(\sqrt{x^(2)+1 })^(2)`

Limits are
`a=1 , b=2`

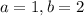
eq. 1 becomes

`V=\int\limits^b_a {\pi  r^(2)\, dx`

`V=\int\limits^2_1 {\pi (f(x) )^(2)\, dx`

`V=\int\limits^2_1 {\pi (\sqrt{x^(2)+1 }  )^(2)\, dx`

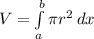
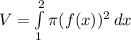
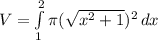
Hence proved.

The volume of the solid formed by revolving the function
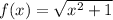`f(x)=\sqrt{x^(2)+1 }` about the x-axis on the interval [1, 2] is given by
`V=\int\limits^2_1 {\pi (\sqrt{x^(2)+1 }  )^(2)\, dx`