The average rate of change is 0
Solution:
The average rate of change of function is given as:
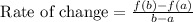
Here the given function is:
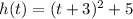
The interval given is
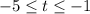
The average rate of change of the function h(t) over the interval
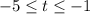 can be calculated as:
can be calculated as:
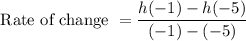
Find h( -5 ) and h( -1 ):
Substitute t = -5 in given h(t)
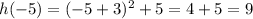
Substitute t = -1 in given h(t)
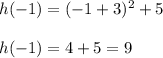
Thus average rate of change is given as:
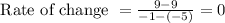
Thus the average rate of change is 0