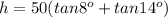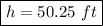Answer:
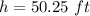
Explanation:
Right Triangles
In a right triangle, one of the internal angles is 90°. When this happens, there is always a longer side, called hypotenuse and two shorter sides, called legs. They relate to Pythagoras's theorem. The basic trigonometric relations also stand, including
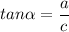
where a is the opposite leg to
 and c is its adjacent led .
and c is its adjacent led .
In our problem, we have a statue being looked by a person in such a way that the top of the statue forms an angle of 8° with the horizontal and the base of the statue forms an angle of 14° down. We also know the distance from the person to the statue is 50 ft. The situation is shown in the image below.
The height of the statue is h=a+b, where
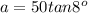
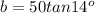
Thus