Question

given the coordinate of one endpoint of AB and it’s midpoint M, find the coordinates of the other endpoint. A(0,9) M(2,5)

Answer 1

The co-ordinate of point B is (4, 1)

Solution:

Given the coordinate of one endpoint of AB and it’s midpoint M , A(0, 9) M(2, 5)

To find: co-ordinate of endpoint B

The midpoint m(x, y) of points
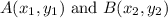`A(x_1, y_1) \text{ and } B(x_2, y_2)` is given as:

`m(x, y)=\left((x_(1)+x_(2))/(2), (y_(1)+y_(2))/(2)\right)`

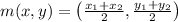
Here in this sum,

`m(x, y) = (2, 5)\\\\A(x_1, y_1) = (0, 9)\\\\B(x_2, y_2) = ?`

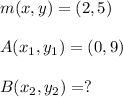
Substituting in above formula, we get

`\begin{aligned}&(2,5)=\left((0+x_(2))/(2), (9+y_(2))/(2)\right)\\\\&(2,5)=\left((x_(2))/(2), (9+y_(2))/(2)\right)\end{aligned}`

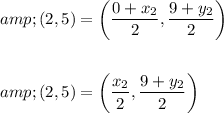
Compare the L.H.S and R.H.S

`2 = (x_2)/(2) \text{ and } 5 = (9+y_2)/(2)\\\\x_2 = 2 * 2 \text{ and } 10 = 9 + y_2\\\\x_2 = 4 \text{ and } y_2 = 1`

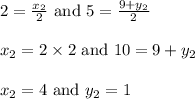
Thus the co-ordinate of point B is (4, 1)