The given system of equations has only one solution
Solution:
Given system of equations are:
2y = x - 9 ------- eqn 1
5x - 4y = 18 ------- eqn 2
Let us first solve the system of equations
From eqn 1,
x = 2y + 9 ----- eqn 3
Substitute eqn 3 in eqn 2
5(2y + 9) - 4y = 18
10y + 45 - 4y = 18
6y = 18 - 45
6y = -27
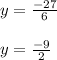
Substitute the value of "y" in eqn 3
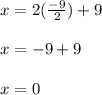
Thus
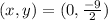
Thus the given system of equations has only one solution