Question

triangle ABC, side AB = 10, side AC = 13, and side BC = 16. What is the measure of the largest angle in degrees?

Answer 1

The largest angle in degrees is 87.13 degrees

Solution:

The figure is attached below

In a triangle ABC,

side AB = 10

side AC = 13

side BC = 16

To find: largest angle in degrees

Angle opposite to longest side is always the largest interior angle

Which means that, the longest side is always opposite the largest interior angle.

Here, longest side is BC

Therefore, angle opposite to BC is angle A i.e
`\angle A`

Apply cosine rule to find angle A

If we know the three sides of the triangle and one angle we can use the cosine rule:

The Cosine Rule states that the square of the length of any side of a triangle equals the sum of the squares of the length of the other sides minus twice their product multiplied by the cosine of their included angle.

Therefore,

`a^2 = b^2 + c^2-2bc \cos A`

`16^2 = 13^2 + 10^2 - 2(13)(10) \cos A\\\\256 = 169 + 100 -260 \cos A\\\\256 = 269 -260 cosA\\\\260 cosA = 269 - 256\\\\260 cosA = 13\\\\cos A = (13)/(260)\\\\cos A = 0.05\\\\A = cos^(-1)(0.05)\\\\A = 87.13`

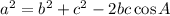
Thus largest angle in degrees is 87.13 degrees